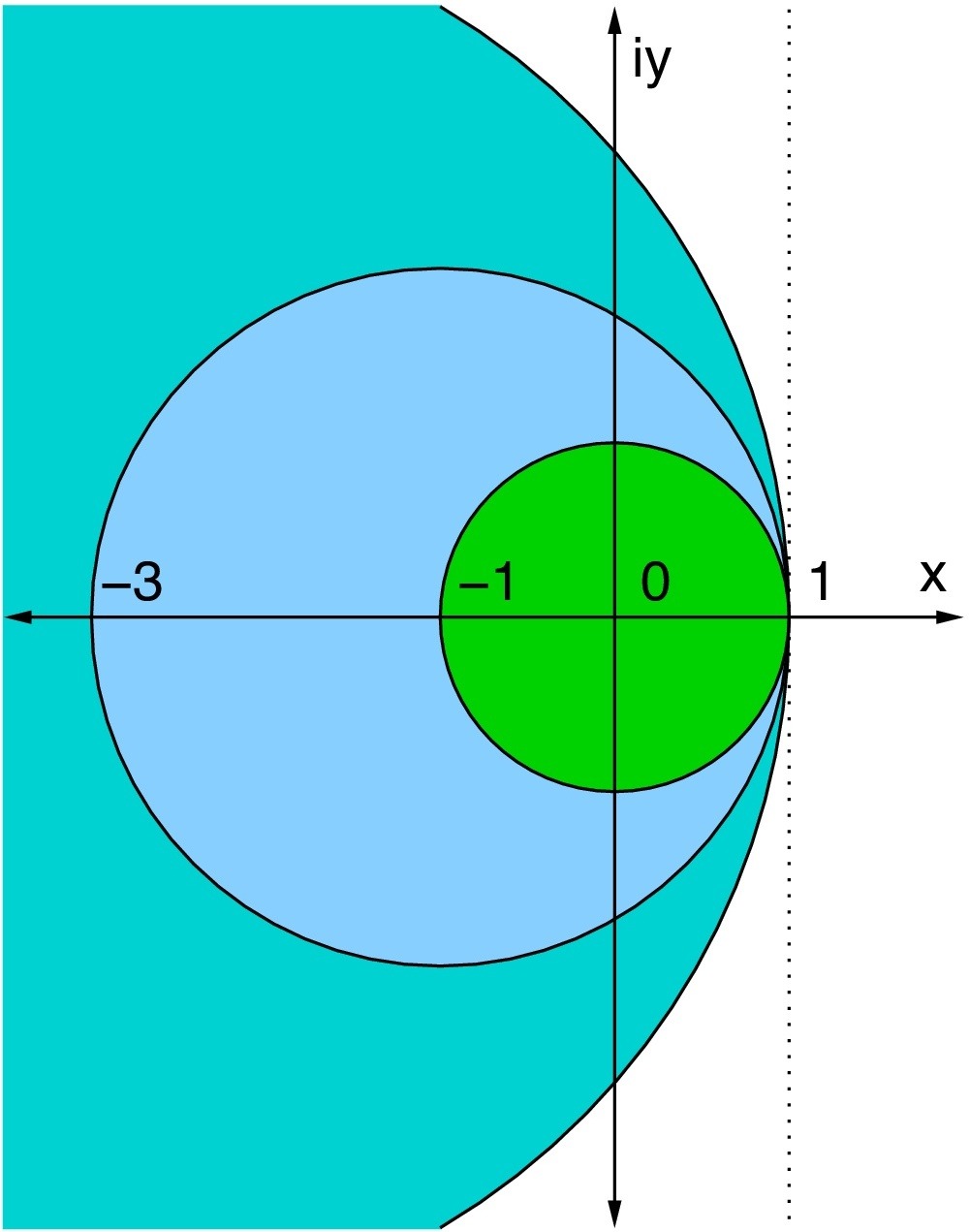
Utility analysis is quite useful in quantifying direct and indirect species relations in a compartmental ecosystems model, regardless of its size or complexity. It serves as a basis for the formulation of system-wide synergism and mutualism measures. A significant issue that limits the applicability of utility analysis is that its mathematical formulation requires the convergence of a matrix power series, which may fail for otherwise perfectly valid ecosystem models. For example, utility analysis for the well known Neuse river estuary nitrogen flow models, collected over 4 years (16 seasons total), do not converge for some seasons, but converge for others. Interestingly, ecologists find the analysis results meaningful and useful, even when the convergence criteria are not satisfied. Caner Kazanci’s work investigates the cause for this divergence, analyzes the properties of the matrix power series, and uses an alternative summability method which transforms the diverging matrix power series into a converging one. In particular, he and his team show that finitely many applications of the Euler transform are capable of forcing convergence on an otherwise diverging matrix power series for utility analysis. While the divergence in the regular sense remains, his work brings forward a strong mathematical argument that the utility analysis, synergism and mutualism indices, are useful for all ecological network models, regardless of their convergence characteristics.
- Kazanci, C., and M. Adams. 2017. Ecological utility theory: Solving a series convergence issue. Ecological Modelling 358:19–24.