Corresponding Author: Eamon B. O’Dea, odea35@gmail.com
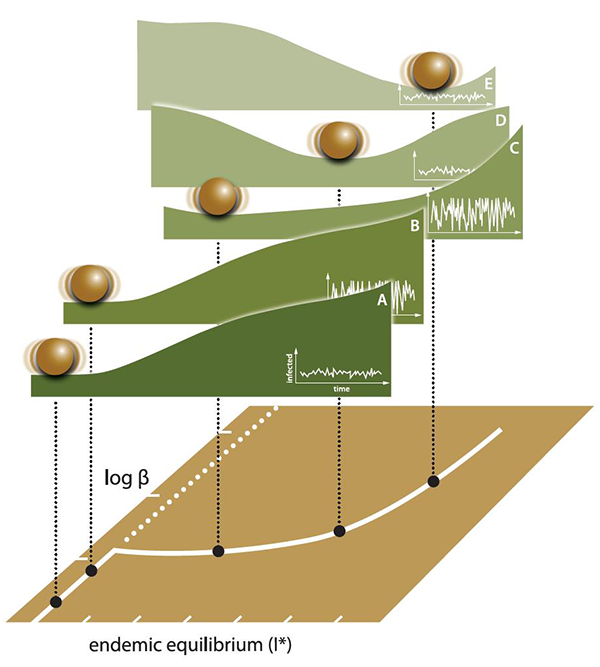
An important component of predicting disease emergence is the ability to assess the distance to epidemic thresholds, the critical number of susceptible hosts needed for an epidemic to occur. Monitoring this threshold allows researchers to confirm the emergence of an epidemic and take action to control its spread. One way to monitor thresholds is to quantify the “slowing down” of dynamics that are characteristic of a particular epidemic threshold. However, this can be difficult. In some disease models, such as the susceptible-infected-recovered (SIR) model, host population dynamics may slow down even when transmission is far from threshold levels. For models such like this, using a single variable to estimate the distance to the threshold may be more viable. In a recent report, CEID members Eamon O’Dea, Andrew Park, and John Drake show how the relative weighting of a variable depends on the covariance of the perturbations to a system with two degrees of freedom. While their results are only accurate for the long-term observation of large systems, they also provide insight into the behavior of estimates from simulations with a range of population sizes, environmental noise, and observation schemes. After formulating these guidelines about when estimates are accurate, they further illustrate that having multiple distance estimates can be used to predict the rate of approach to a threshold. Their results have important implications, such as guiding public health policies, tracking the movement of a system towards a threshold to provide early warnings, and even monitoring external changes to a system that may help control infectious disease outbreaks.